消费者行为在一定程度上受到个体因素的影响,这些个体因素包括用户的性别、年龄、收入、受教育程度、生活方式、自我概念等因素。在消费者行为的研究中,需要考虑这些个体因素的影响。
有些资料上说“在进行独立样本T检验之前,要先对数据进行正态性检验,满足正态性才能进一步分析。” 但是有些人口统计变量(那些个体因素)是压根就不符合正态性的,比如性别,但这时候很多论文仍然会进行独立方差T检验,所以“满足正态性”这个前提可以不考虑了。
比如要检验性别是否会影响用户对APP的持续使用意愿:
点击“分析”-“比较平均值”-“独立样本T检验”
把要检验的变量——持续使用意愿放在检验变量(T)那个框里,将性别放在分组变量中。
检验结果如下:
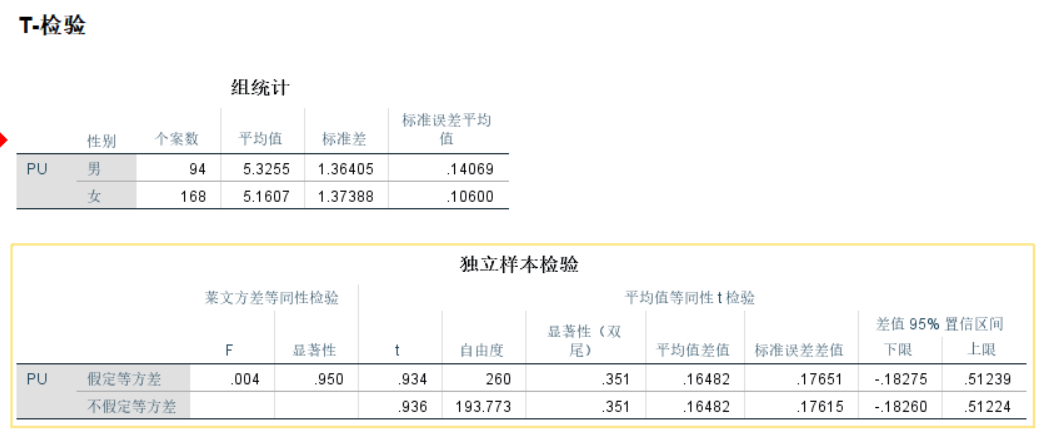
看上图中的黄色框里“独立样本检验”表格,先看左侧部分——莱文方差等同性检验(也叫F检验,或Levene的变异数相等测试),上下两行分别为假定方差相等和假定方差不相等,对应两种情况:
若方差相等,即不显著(>0.05),看第一行的t检验结果(第一行右侧显著性部分)
若方差不相等,即显著(<0.05),看第二行的t检验结果(第一行右侧显著性部分)
上图中是0.95>0.05,不显著,看第一行的t检验结果。
t检验部分的显著性才是性别是否会影响用户对APP的持续使用意愿的最后判断依据,上图中的0.351>0.05,即不显著,无差异。即性别不会影响用户对APP的持续使用意愿。
进一步理解,在例子中,假设方差相等,即男性和女性的持续使用意愿的方差是相等的,看与F值对应的显著值为0.95,即男性和女性的持续使用意愿的方差是相等这一假设的可能性有0.95,大概率事件,接受原假设。
再看方差相等这一行的t值对应的显著性(双尾)为0.351,即男性和女性的持续使用意愿均值没有显著差异这个假设出现的概率有0.351,大概率事件(小概率事件是概率<0.05),接受原假设,所以男性和女性的持续使用意愿均值没有显著差异。
另外,独立样本T检验主要用于分析控制变量在两个不同水平时因变量的均值是否存在显著差异。因此,当控制变量的分层大于2时,比如年龄分组:A:19岁及以下 B:20-29岁 C:30-39岁 D:40-49岁 E:50岁及以上 这时独立样本T检验就可以换成单因素方差分析。
单因素方差分析主要用于分析单一控制因素在不同水平(不限于两个)时因变量的均值是否存在显著性的差异。